ГБОУ СПО Пензенский
профессионально — педагогический колледж
Курсовая работа
Тема: Актуальные
методы и приемы, позволяющие осознанно решать задачи
Пенза, 2010 г.
Введение
В общей системе
обучения математике решение задач является одним из видов наиболее сложных и
эффективных упражнений. Решить задачу — значит раскрыть связи между данными и
искомым, заданные условием задачи, на основе чего выбрать, а затем выполнить
арифметические действия и дать ответ на решение задачи. Решение задач имеет
чрезвычайно важное значение прежде всего для формирования у детей полноценных
математических понятий, для усвоения ими теоретических знаний, определяемых
программой. Задачи являются тем конкретным материалом, с помощью которого
формируются у детей новые знания и закрепляются в процессе применения уже
имеющиеся. Сам процесс решения задач оказывает значительное положительное влияние
на умственное развитие школьников, поскольку он требует выполнения умственных
операций: анализа и синтеза, конкретизации и абстрагирования, сравнения и
обобщения.
Процесс обучения
решению задачи наиболее сложны период обучения математике. В настоящее время
дети обучаются по различным программам, которые дополняются и усложняются,
значит, должна совершенствоваться методика обучения решению задач. Появляются
новые методы, объединяя в себе опыт прошлого и современные разработки. Решением
проблемы обучения решения задач занимались Н.Б. Истомина, М.И. Моро, А.М.
Пышкало и др. Они пришли выводу, что вопрос о том, как научить детей
устанавливать связи между данными и искомыми в текстовой задаче и в
соответствии с этим выбрать, а затем выполнить арифметические действия,
решается по- разному, с помощью различных методов и приемов. Цель курсовой
работы – изучить, какие актуальные методы и приемы решения задач, используемые
в современных начальных школах, позволяющие детям осознанно решать задачи. Для
раскрытия цели сформулированы следующие задачи:
1.
Раскрыть
формирование учебных умений младших школьников в процессе обучения решению
текстовых задач.
2.
Рассмотреть
метод варьирования текстовых задач как средство повышения осознанности знаний
учащихся начальных классов.
3.
Рассмотреть
развитие математического мышления учащихся посредством решения эвристических
задач.
Формирование учебных
умений младших школьников в процессе обучения решению текстовых задач
Обучение предполагает
не только овладение учащимися определенной суммой знаний и умений, но и
формирование общеучебных умений, которые связаны с самостоятельным получением
знаний и их применением в практической деятельности. В публикациях, посвященных
общеучебным умениям, приведены их разные классификации. Наш многолетний опыт
работы в начальной школе свидетельствует, что удобнее использовать традиционное
выделение следующих общеучебных умений: учебно-организационные,
учебно-информационные и учебно-интеллектуальные. Часто к ним добавляются еще и учебно-коммуникативные
умения.
К
учебно-организационным относят умения:
— намечать
задачи деятельности и рационально планировать их выполнение;
— создавать
условия, обеспечивающие успешное выполнение работы (режим дня, организация
рабочего места);
— работать
в заданном темпе;
— осуществлять
самоконтроль и самоанализ учебной деятельности;
— оценивать
учебную деятельность. Под учебно-информационными понимают умения работать с
учебной книгой и с основными компонентами учебника (оглавлением, вопросами,
заданиями к учебному тексту, приложениями, образцами, схемами, таблицами и
т.п.), а также осуществлять наблюдения.
Учебно-интеллектуальные
умения — это главные и вместе с тем самые сложные умения, поскольку
они связаны с развитием таких качеств мышления, как глубина, гибкость,
устойчивость, самостоятельность. Уровень интеллектуального развития учащегося
определяется главным образом степенью сформированности умений:
—оценивать
свои знания и осознавать необходимость новых знаний;
—добывать
новые знания;
—приобретать
полученные знания (анализировать, синтезировать, обобщать, классифицировать,
сравнивать, выделять причины и следствия) для необходимого результата;
—преобразовывать
информацию из одной формы в другую (текст, таблица, схема, график, иллюстрация
и др.) и выбирать наиболее удобную для себя форму;
—передавать
содержание информации в сжатом или развернутом виде.
Учебно-коммуникативные
умения — это умения, которые формируются и используются в
учебной работе и в процессе общения людей друг с другом; более того, развитые учебно-коммуникативные
умения помогают общению, делают его более содержательным, интересным,
целенаправленным. К ним относятся умения:
—слушать
(одно из самых трудных умений, требующее сосредоточенности, равномерного
распределения внимания на довольно большой период времени);
—слушать
и одновременно записывать;
—читать
текст и одновременно слушать инструктаж о работе над ним;
—выражать
литературным языком свои мысли, пользоваться специальным языком той науки,
которая лежит в основе учебного предмета;
—доносить
свою позицию до других, владея приемами монологической и диалогической речи;
—задавать
вопросы;
—аргументировать
и доказывать.
Общеучебные
умения и навыки являются универсальными способами получения и применения знаний
и создают условия для формирования у младшего школьника практических навыков
осуществления учебной деятельности, что, в свою очередь, способствует
формированию общего умения учиться.
Охарактеризуем
возможности формирования общеучебных умений при решении текстовых задач в
учебно-методическом комплекте Н.Б. Истоминой. Н.Б. Истомина рассматривает
процесс решения задач (простых и составных) как переход от словесной модели к
математической. В основе этого перехода лежит семантический (смысловой) анализ
текста и выделение в нем математических понятий и отношений (математический
анализ текста). Учащиеся должны быть подготовлены к этой деятельности, поэтому
знакомство с текстовой задачей следует проводить после специальной работы по
формированию математических понятий и отношений, которые будут использованы при
решении задач. До знакомства с решением задач ученики должны достигнуть
определенного уровня развития логических приемов мышления (анализа и синтеза,
сравнения, обобщения), а также приобрести определенный опыт в соотнесении
предметных, текстовых, схематических и символических моделей, который может
использоваться для интерпретации текстовой модели. Таким образом, готовность
школьников к знакомству с текстовой задачей предполагает определенный уровень
сформированности:
1)
навыков чтения;
2) представлений
о смысле действий сложения и вычитания, их взаимосвязи, о понятиях увеличить
(уменьшить) на, о разностном сравнении;
3) основных
мыслительных операций (анализа, синтеза, сравнения);
4)
умения описывать предметные ситуации и переводить их на язык схем и
математических символов;
5)
умения чертить, складывать и вычитать отрезки;
6)
умения переводить текстовые ситуации и схематические модели.
В
отличие от других авторов учебников, Н.Б. Истомина впервые вводит понятие текстовой
задачи только в третьей четверти I
класса. Происходит это при изучении темы «Увеличить на… Уменьшить на…
Состав однозначных чисел». В задании: «На одной тарелке 9 яблок, а на другой —
на 2 яблока меньше. Обозначь каждое яблоко кругом и покажи на рисунке, сколько
яблок на каждой тарелке»- вербальная модель впервые переводится в предметную,
но здесь учащиеся еще не знакомятся с термином «задача», с ее структурой и
решением, а только готовятся к этому. Выполнение этого задания направлено на
формирование у учащихся нескольких видов общеучебных умений. Это и учебно-организационные
умения: понимать действие, сравнивать полученный результат (в данном случае в
виде условного рисунка) с задачей, оценивать свою учебную деятельность и
деятельность в данном случае героев учебника, Маши и Миши (далее в учебнике
предлагается оценить, кто из них правильно выполнил условный рисунок, и
сравнить со своим вариантом). Это и учебно-информационные умения: сознательно и
правильно читать текст с соблюдением норм литературного произношения,
логических ударений, пауз; осуществлять качественное и количественное описание
компонентов объекта после наблюдения. Это и учебно-интеллектуальные умения: перерабатывать
знания (анализировать, обобщать, сравнивать) для необходимого результата,
преобразовывать информацию из одной формы (вербальной или письменной) в другую
(иллюстративную).
При
изучении темы «Число и цифра О» первоклассники продолжают выполнять подготовительные
упражнения к решению текстовых задач. Одно из них такое: «Петя сделал 7
корабликов и З из них подарил Саше. Обозначь каждый кораблик квадратом и
покажи, сколько корабликов Петя подарил Саше и сколько корабликов у него
осталось». В ходе выполнения этого упражнения, а именно обозначения корабликов
квадратами, у школьников формируется учебно-информационное умение строить
простейшие модели после осуществления наблюдения. Далее автор учебника
предлагает вновь определить, кто из героев учебника (Маша или Миша) правильно
выполнил задание. Сравнение приведенных здесь условных рисунков способствует
формированию таких качеств ума, как глубина, гибкость, устойчивость,
самостоятельность, т.е. формированию учебно-интеллектуальных умений.
Тема
«Сложение и вычитание отрезков» полезна для учащихся I
класса не только в плане формирования обобщенных представлений о конкретном
смысле сложения и вычитания, но и для осознанного использования схем при
решении задач. Одно из заданий этой темы звучит так: «Подумай! Как начертить
отрезок, равный разности отрезков АВ и CD?»
Герои
учебника Маша и Миша предлагают свои решения, а учащиеся должны объяснить, кто
из них прав. Выполнение этого задания помогает формированию следующих умений:
а)
учебно — коммуникативных (выражать мысли на языке математики, аргументировать и
доказывать);
б)
учебно-интеллектуальных (перерабатывать знания для необходимого результата,
преобразовывать информацию);
в)
учебно-организационных (осуществлять самоконтроль и самоанализ своей учебной
деятельности, оценивать свою деятельность и деятельность других).
При
изучении темы «На сколько…?» в учебнике встречаются задания, выполняя которые
учащиеся должны соотнести предметную модель с математической (равенством). Эти
упражнения нацелены на усвоение смысла действий сложения и вычитания понятия
разностного сравнения и являются подготовительными к решению текстовых задач.
Одно из таких заданий: «В букете 4 желтых розы и 5 белых.
Второклассники
учатся показывать решение текстовых задач уже не только с помощью
символического рисунка, но и рисунками-схемами. Выполняя задание: «Карандаш
длиннее ручки на 2 см. Догадайся, как показать это, пользуясь отрезками», учащиеся
самостоятельно приходят к правильному ответу, опровергая высказывания героя
учебника Маши, которая думает, что это нельзя сделать, ведь неизвестна длина
ручки. Ученики соглашаются с другим персонажем учебника (Мишей) в том, что
длину ручки знать не нужно и что соотношение длин можно показать с помощью
отрезков. Нетрудно видеть, что в данной ситуации у учащихся формируется умение
преобразовывать одну информацию в другую, передавать содержание задания в
сжатом виде, что способствует формированию учебно -методических умений. При
работе над задачей: «У Вовы 74 марки, а у Миши на 8 марок больше. Каким отрезком
обозначены марки Вовы? Каким отрезком — марки Миши? Построй отрезок, который
будет показывать, сколько марок у Вовы и Миши вместе. Построй отрезок, который
будет показывать, на сколько марок у Миши больше, чем у Вовы» у учеников
формируются все виды общеучебных умений:
а)
учебно-организационные (соблюдение последовательности действий, использование
учебных принадлежностей);
б)
учебно-информационные (работа с вопросами и заданиями к учебному тексту;
осуществление наблюдения объекта в соответствии с целями и способами,
предложенными учителем);
в)
учебно-интеллектуальные (в большей степени анализ и синтез, в меньшей —
сравнение).
Во
второй четверти II класса учащиеся
знакомятся со структурой задачи, с записью ее решения и ответа. Эта работа
начинается с формирования умения читать текст задачи, т.е. устанавливать
взаимосвязь между ее условием и вопросом. С этой целью в учебниках включены
специальные задания на сравнение, преобразование и конструирование, т.е. на формирование
учебно-интеллектуальных умений. Если при подготовке к решению текстовых задач в
учебнике уделяется больше внимания формированию таких умений, как анализ и
синтез, то при знакомстве со структурой задачи развиваются умения сравнивать,
обобщать и классифицировать.
Таким
образом, при обучении младших школьников решению задач формируются такие
специальные умения, как умение читать текст задачи, устанавливать взаимосвязи
между условием и вопросом, данным и искомым, выбирать арифметическое действие
для решения, а также развиваются и общеучебные умения. Следовательно, при
подготовке к уроку математики учитель должен продумать, какие общеучебные
умения следует формировать в ходе организации той или иной формы работы.
Метод
варьирования текстовых задач как средство повышения осознанности знаний
учащихся начальных классов
Особую
актуальность в настоящее время имеет развивающая парадигма образования. На
первый план выдвигаются личностные достижения ученика, а знания рассматриваются
как средство развития. Процесс обучения должен способствовать формированию осознанных
и прочных знаний учащихся, которые, в свою очередь, являются движущей силой
развития потенциала личности и необходимым условием предметной и
интеллектуальной компетентности как нового результата школьного образования.
Педагоги
И.Я. Лернер, М.Н. Скаткин, В.В. Краевский рассматривают следующие показатели
качества знаний: полноту и глубину, свернутость и развернутость, конкретность и
обобщенность, оперативность и гибкость. Они являются предпосылками и
необходимыми условиями формирования качеств, стоящих как бы на вершине пирамиды
знаний, а именно осознанности и прочности. В методике обучения математике
осознанность знаний рассматривается преимущественно как умение школьников
обосновывать решение задач, а проверяется осознанность и прочность по умению
решать задачи. Решение текстовых задач является одним из наиболее эффективных
средств, реализующих цель образования, связанную с формированием инициативной,
творческой личности, так как только при решении текстовых задач реализуются все
три этапа применения математики: формализации знаний; решения задачи внутри
построенной математической модели; интерпретации полученного решения задачи
(В.В. Фирсов).
В
качестве одного из важных средств формирования осознанных и прочных знаний по
математике можно использовать разработанный метод варьирования текстовых задач
как способ конструирования учебного материала и как метод организации учебной
деятельности учащихся. Выделяются следующие основные свойства осознанности, которые
целесообразно формировать при обучении математике: осмысление связей и
отношений между знаниями; осознание одних знаний как базовых для других знаний.
Это позволило в ходе исследования конструировать эти связи и отношения между
текстовыми задачами, а также выделять или составлять 11 базовую (основную)
задачу по теме. В результате было сформулировано определение метода
варьирования текстовых задач и определение базовой задачи.
Метод
варьирования текстовых задач — это способ конструирования из
одной задачи (назовем ее базовой) цепочки взаимосвязанных задач.
Опираясь
на обязательные результаты обучения математике и учитывая математическую
подготовку класса, изначально выбираем или конструируем базовую (основную)
задачу по теме. Базовая задача — это задача с несложными математическими
зависимостями, заданными явно. Решение этой задачи необходимо для решения
других задач по теме. Базовая задача по теме служит подготовительной,
«трамплинной» задачей для решения всех последующих сконструированных задач.
Каждая новая задача соотносится и с базовой задачей, и с ранее составленными
задачами. Организуя коллективную познавательную учебную деятельность учащихся
по конструированию задач, педагог широко использует активность и инициативу
самих учеников в данном виде деятельности. Формирование осознанных и прочных
знаний при решении текстовых задач происходит в процессе преобразующей учебной
познавательной деятельности, в ходе конструирования на уроке, на глазах у
учащихся цепочек взаимосвязанных задач с помощью метода варьирования текстовых
задач. Повышение осознанности и прочности знаний достигается через установление
связей между задачами (в сконструированной цепочке задач), через осмысление
учащимися важности умения решать базовую задачу, за счет формирования у
школьников мыслительной операции преобразования в ходе изменения структуры
задачи и ее формы предъявления.
На
основании теоретического анализа методической литературы и многолетнего опыта
работы нами выделены следующие приемы варьирования текстовых задач.
Прием
1. Изменение
сюжета задачи и (или) числовых значений величин задачи.
Прием
2. Изменение
математических зависимостей между величинами, заданными в условии.
Прием
3. Добавление
данных в условие задачи при том же требовании.
Прием
4. Изменение
(добавление) требований задачи при том же условии .
Прием
5. Составление
обратных задач.
Прием
6. Составление
задач с недостающими или избыточными данными.
Перед
характеристикой отдельных приемов варьирования задач остановимся на кратком
анализе уровней осознанности знаний.
Опираясь
на разработанные уровни осознанности знаний в педагогике (М.Н. Скаткин, В.В.
Краевский), психологический подход к показателям качества знаний (умение
осуществлять переходы между предметным, знаковым и модельно-образным планом
содержания знаний), а также учитывая важность операции преобразования для формирования
осознанных знаний, разработали уровни осознанности знаний при решении текстовых
задач.
Первый
уровень осознанности
характеризуется умением воспроизвести знания по образцу, т.е. в стандартной
ситуации. Поэтому в исследовании для проверки сформированности умений первого
уровня осознанности конструируется текстовая задача, аналогичная базовой задаче
по выбранной теме. Ученик осуществляет переход между предметным планом (текст
задачи), модельно-образным (схема задачи, краткая запись текста задачи) и
знаковым (математическая модель задачи) планами содержания знаний, что
удовлетворяет психологическим требованиям к диагностическим работам,
направленным на проверку осознанности знаний (В.А. Львовский).
Второй
уровень осознанности
характеризуется умением проводить операцию сравнения, противопоставления,
обобщения, умением интерпретировать и доказывать. Поэтому конструирование
задачи 2 для проверки сформированности умений второго уровня осознанности
осуществляется на основе преобразования зависимостей в структуре задачи 1.
Усложнение структуры задачи проводится за счет изменения первоначальных
взаимосвязей в базовой задаче, за счет введения дополнительных элементов в
условие задачи, в требование задачи, т.е. за счет применения второго, третьего
и четвертого приемов варьирования. В математически подготовленном классе
возможно предъявление схемы задачи обратной структуры с использованием пятого
приема варьирования.
Третий
уровень осознанности
характеризуется наличием умений первых уровней, а задачи данного уровня
осознанности должны содержать преобразование и включение новых знаний в уже
имеющиеся структуры. Поэтому конструирование задачи 3 для проверки
сформированности умений третьего уровня осознанности осуществляется с помощью
второго, третьего, четвертого и пятого приемов варьирования. Сконструированная
задача 3 предъявляется ученикам в знаковом плане, т.е. в виде математической
модели. Ученик осуществляет переход между знаковым, модельно-образным и
предметным планами содержания знаний. Он должен сравнить математическую модель
предложенной задачи с математической моделью предыдущей задачи и преобразовать
содержание задачи 2 так, чтобы оно соответствовало предложенной математической
модели. На третьем уровне осознанности кроме отработанных умений предыдущих
уровней формируются следующие умения: переводить задачу из абстрактного плана в
конкретный план; интерпретировать абстракцию — математическую модель задачи,
т.е. разбивать математическую модель на подзадачи и соотносить их с текстами и со
схемами предыдущих задач; сравнивать, сопоставлять предложенную математическую
модель задачи с математическими моделями решенных ранее задач; привести в
соответствие факты действительности (текст задачи, схему задачи) с
теоретической интерпретацией (математическая модель задачи); проводить анализ
через синтез всей сконструированной цепочки задач, делать обобщения.
Задачный
материал к каждому приему варьирования должен удовлетворять разработанным
уровням осознанности знаний, способствовать созданию в сознании учащихся
правильного взаимоотношения между содержанием задач и их внешним выражением
(предметным, знаковым, модельно-образным).
В
начальных классах широко используется первый прием варьирования текстовых
задач, на характеристике которого остановимся подробнее.
Выделив
уровни осознанности знаний учащихся, мы отметили, что первый уровень
осознанности знаний предполагает умение применять знания по образцу, в схожей
ситуации. В обучении решению задач с помощью метода варьирования ученики
достигают первого уровня осознанности знаний, если могут самостоятельно решить
базовую задачу или аналогичную ей. Данный прием варьирования как раз и
предполагает: изменяя сюжет задачи и (или) изменяя числовые значения данных,
школьники получают задачу, аналогичную базовой. Таким образом, применяя первый
прием варьирования, можно сформировать у школьников знания на первом уровне
осознанности.
Исследуя
пути повышения качества усвоения знаний по математике в начальной школе, Н.А.
Менчинская и Д.Н. Богоявленский предостерегали от возможности формирования
стереотипа при решении задач и предлагали для снятия данного недостатка
выполнять некоторые правила. Анализируя рекомендации данных авторов
применительно к формированию осознанности знаний школьников, сформулированы
следующие требования, которых нужно придерживаться при составлении задач первым
приемом варьирования.
Требование
1. Изменяя
сюжет (фабулу) задачи, желательно применять различные глаголы для описания
операций, выполняемых заданным действием, например, отдали, отнесли, потеряли,
съели, истратили и т.д.
Требование
2. Изменяя
сюжет задачи, необходимо следить, чтобы определенные данные не присутствовали в
задачах в постоянном сочетании. Если это требование не соблюдать, то школьники,
решая задачу по аналогии, проводят сразу привычный синтез, игнорируя анализ
задачи. Например, рассмотрим задачи 1 и 2.
Задача
1. В первой цистерне 11О т нефти. Во второй цистерне нефти больше, чем в
первой, в 4 раза. Сколько нефти в двух цистернах вместе?
Задача
2. В первой корзине было в 4 раза больше слив, чем во второй. Сколько
килограммов слив было вместе в двух корзинах, если во второй было 12 кг?
Во
второй задаче при изменении сюжета взаимосвязь между данными (в 4раза больше) осталась
прежней. Однако здесь видны два изменения: во-первых, поменялись местами
известное количество и неизвестное (стало известно количество слив во второй
корзине, а не в первой); во-вторых — отношение в 4 раза больше поставлено на
первое место, а известное количество слив во второй корзине встроено в вопрос
задачи, что потребует от ученика умения вычленить это данное из вопроса задачи,
т.е. провести анализ, а не решить задачу по образцу.
Требование
3. Изменяя
сюжет задачи, необходимо фиксировать связи между величинами не только в явной,
но и в косвенной форме.
Приведем
примеры.
Задача
1. В первой коробке 27 карандашей. Сколько карандашей в трех коробках вместе,
если во второй коробке в 3 раза меньше карандашей, чем в первой, а в третьей
коробке на 17 карандашей больше, чем во второй коробке?
Задача
2. В первом ящике 57 кг яблок, во втором ящике в 3 раза меньше, чем в первом и
на 17 кг меньше, чем в третьем ящике. Сколько килограммов яблок вместе в трех
ящиках?
Требование
4. Меняя
числовые данные в задаче, некоторые из них можно записывать в словесной форме.
Так, вместо «в 3 раза», можно записать «в три раза». Это приучает учащихся
осмысливать текст задачи, а не пользоваться чисто внешними проявлениями и
соотносить между собой только данные, записанные цифрами.
Требование
5.
Переводить задачи из конкретного плана в абстрактные значения (заменять
числовые величины буквенными). Эта форма работы важна, особенно в IV-V
классах, так как она приучает учащихся самостоятельно «переводить» на язык
математических терминов различные соотношения, записанные в конкретной
жизненной форме. Приведем пример.
Задача
1. Купили 10 тетрадей по 7 р. и 8 карандашей по 4 р. Сколько стоит вся покупка?
Задача
2. Цена тетради а копеек, а карандаша b
копеек.
Сколько надо заплатить за х тетрадей и у карандашей?
Здесь
обобщение рассматривается как переход от конкретного плана к абстрактному
плану.
Требование
6. Перевод
задачи из абстрактного плана в конкретный план. Например, дана задача: «Сумма
двух чисел равна а, одно число больше другого на b.
Найти
эти числа». Конкретизируем задачу, придумав в ходе коллективной деятельности
сюжет: «У Васи и Коли вместе 20 орехов, причем у Васи больше, чем у Коли, на 4
ореха. Сколько орехов у каждого мальчика?»
Выполняя
описанные выше требования конструирования задач с 16 помощью первого приема
варьирования, педагог активизирует процесс мышления учащихся (за счет
продуманного преобразования структуры задачи), а не только формирует
репродуктивную деятельность, в ходе которой, как известно, перегружается
память, что приводит к повышенной утомляемости и утрате интереса к обучению
[4].
Первый
прием варьирования используется учителем в основном как механизм построения
текстовых задач. В меньшей степени он подходит для организации преобразующей
деятельности учащихся на уроке, которую целесообразно развивать при
конструировании задач с помощью остальных приемов варьирования. Рассмотрим
использование второго и шестого приемов варьирования для конструирования
цепочки взаимосвязанных задач по теме «Периметр и площадь прямоугольника».
Технология
составления упражнений с недостающими данными проста: из обычной учебной
текстовой задачи учитель убирает одно данное. Далее работа с задачей на уроке
может быть построена разными способами.
Способ
1: доопределить условие задачи, используя субъектный опыт учащихся и ранее
приобретенные знания.
Способ
2: доопределить условие задачи, используя таблицы, графики, диаграммы.
Способ
3: оставить задачу с неполным условием и получить исследовательскую задачу, так
как она будет иметь неоднозначное решение [3].
Рассмотрим
работу с такой задачей третьим способом. Предварим составление задачи с
неполными данными составлением трех задач с использованием второго приема
варьирования.
Задача
1 (базовая, первый уровень осознанности). Длина прямоугольника равна 9 см, а
его ширина на 6 см меньше длины. Найти периметр и площадь данного
прямоугольника. Составь краткую запись (схему) задачи, запиши решение по
действиям.
Задача
3 (третий уровень осознанности). По равенству Р = (5 + (5 + 2) • 2 составь
задачу с похожим сюжетом. Выполни краткую запись задачи, запиши ее решение по
действиям, составь равенство для нахождения периметра прямоугольника, сравни
полученное равенство с данным. На равенство в какой задаче похоже данное
равенство? Чем отличается равенство задачи 3 от равенства задачи 1 ? Как
изменится текст задачи 3 по сравнению с задачей 1?
При
составлении задачи по равенству внимание учащихся направлено на анализ зависимостей
между величинами, определяемых данным выражением. Это, в свою очередь,
оказывает положительное влияние и на те случаи, когда впоследствии учащиеся
самостоятельно будут решать готовые задачи, так как они осознанно вникли в
структуру задачи, разложив на составные части данное выражение и восстановив
взаимосвязи между сторонами прямоугольника. Использование второго приема
варьирования при составлении данной цепочки задач позволяет школьникам
проводить постепенное сокращение промежуточных звеньев рассуждений при решении
последующих задач.
– Чем
похожи задачи 1, 2 и 3? (Одинаковый периметр.) Какая площадь у этих
прямоугольников? (Разная.) Сколько существует прямоугольников с периметром 24
см?
Таким
образом, в ходе беседы получена задача 4 с неполным условием: «Периметр
прямоугольника 24 см. Найти его площадь».
– Сколько
решений этой задачи уже получено? Выпишем их.
Если
при решении данной задачи возникают затруднения, то учитель может задать
наводящий вопрос: «Чему равна сумма длины и ширины?» На доске и в тетрадях
учащихся появляются записи.
школьник умение математический текстовый задача
Р=(9
+ 3) • 2, S = 27.
Р=(8
+ 4) • 2, S=32.
Р=(7
+ 5) • 2, S=35.
Р=(11
+ 1) • 2, S=11.
Р=(10
+ 2) • 2, S=20.
Р=(6
+ 6) • 2, S=36.
Ответ:
задача имеет 6 решений.
Осуществляя
перебор возможных вариантов, учащиеся проводят элементы исследовательской
деятельности и отвечают на вопросы: «У какого прямоугольника самая большая
площадь? Как его можно назвать по-другому?» В старших классах мы докажем, что
из всех прямоугольников с заданным периметром наибольшую площадь имеет квадрат.
Используя данный факт, можно решить практическую задачу 5: «Для ограждения
дачного участка купили 92 м сетки. Какой формы участок выгоднее обнести этой
сеткой? Чему равна площадь такого участка?»
Если
задачу 4 дать без предварительно решенной цепочки из трех задач, то это будет
исследовательская задача. Решение трех предварительных задач позволило включить
в исследовательскую деятельность всех учащихся класса, так как эти три задачи
играли роль подзадач, а исследовательская задача возникла естественным путем на
заключительном этапе их решения. Таким образом, при конструировании такой
цепочки задач возможно формирование осознанных знаний всех рассмотренных трех
уровней.
Упражнения
должны формулироваться учителем так, чтобы их выполнение требовало
самостоятельной мысли ученика, т.е. было направлено на творческий поиск
ученика. Именно такой подход использует в своей работе учитель начальных
классов школы № 249 Санкт-Петербурга Е.В. Милейко, работающая по программе
«Школа 2100». Рассмотрим, как она использовала групповую работу на уроке
математики в III классе при изучении
темы «Скорость, время, расстояние» на этапе закрепления материала.
Каждая
группа получила конверт, в котором находились 8 листов бумаги. На четырех из
них были записаны задачи с недостающими данными, а на четырех — сами
недостающие данные. Ученики должны были собрать задачи и решить их.
Задачи
с недостающими данными
1.
Длина садовой дорожки равна 120 м. Сколько метров проползала черепаха за одну
минуту?
2.
Длина садовой дорожки равна 120 м. Сколько метров пробегала собака за одну
секунду?
3.
Длина садовой дорожки равна 120 м. Какова ширина дорожки?
4.
Длина садовой дорожки равна 120 м. Во сколько раз дорожка длиннее моста?
Недостающие
данные задач
1.
Черепаха проползла этот путь за 40 мин.
2.
Собака пробежала этот путь за 40 с.
3.
Ее ширина в 40 раз меньше.
4.
Длина моста 40 м.
Во
время коллективной проверки сконструированные задачи прочитываются вслух,
высказываются замечания, возражения по составлению задач.
– Есть
ли среди данных задач такие, в которых требуется найти скорость? Почему вы так
решили? Чем похожи эти задачи? Чем они отличаются?
После
высказываний учащихся предлагается следующее задание:
– Маша,
Катя, Толя и Вася решали каждый только одну из предложенных задач и получили
следующие результаты.
На
доске открывается запись: 3 м/мин, 31 м/с, 3 м, 3 раза.
– Можно
ли определить, кто какую задачу решал? Соотнесите данные ответы с каждой из
предложенных задач.
Обобщение
изученного материала проходит через составление и решение задачи: на подбор
соответствующего данного.
Педагог
предлагает вписать недостающую часть условия следующей задачи: «Длина ветки
равна 90 см. Ответ: скорость муравья 30 см/мин» и сформулировать вопрос.
Деформированные
упражнения с недостающими данными, предложенные учителем на уроке, способствуют
становлению гибкости мышления, что обусловливает, в свою очередь, формирование
осознанных и прочных знаний учащихся.
Развитие
математического мышления учащихся посредством решения эвристических задач
На
первых занятиях для самостоятельного решения всем детям предлагалась одна и та
же задача. После того как дети познакомились с особенностями решения задач
каждого вида, методика работы была изменена. На последующих занятиях
раздавались индивидуальные карточки, например:
Карточка-задание
№ 1
1.
В доме живут Коля и Наташа. Около дома гуляет только Наташа. Где Коля?
2.
На сколько минут ты опоздаешь в школу, если твои часы будут отставать на 10
минут, а ты думаешь, что они спешат на 10 минут, и вышел из дома так, чтобы
прийти точно?
3.
У Толи на 8 яблок больше, чем у Оли. Сколько яблок должен Толя отдать Оле,
чтобы яблок у них стало поровну?
4.
Как отмерить 1 л воды, если есть кружки емкостью 5 л и 2 л?
5.
Какое слово лишнее и почему:
а) лошадь,
корова, волк, кошка, собака;
б) молоко,
масло, сало, сливки, простокваша.
6. Нарисуй
отдельно простые фигуры, из которых состоит эта фигура:
Наиболее
успешно дети справлялись с решением задач логического типа, в которых им был
хорошо знаком или материал (числа, геометрические фигуры, конкретные предметы),
или операции (анализ признаков геометрических фигур, продолжение
последовательности чисел с определенной закономерностью чередования и др.).
Задачи, требующие исключительно внутреннего плана действий, установления
сложных отношений, перестановки и комбинирования простых элементов, перебора
вариантов, решались на первых порах с большим трудом. Однако следует отметить,
что именно эти действия особенно заметно прогрессировали в процессе работы.
За
время занятий отношение детей к эвристическим задачам, а также к другим
заданиям по математике существенно изменилось. Значительно повысился интерес к
обучению. Подход к решению любых задач стал более гибким и самостоятельным.
Рассуждения стали более последовательными и доказательными. Особенно заметно
развился навык учащихся по решению задач, имеющих несколько вариантов
правильных ответов, и задач с использованием активного поиска решения методом
перебора вариантов отношений.
На
наш взгляд, для детей младшего школьного возраста одним из эффективных
дидактических средств, способствующих формированию гибкости мышления, являются
также дидактические игры, логические и занимательные задачи, головоломки,
которые составлены на основе знания законов мышления и в которых догадке как
способу решения предшествует тщательный анализ существенных признаков.
Покажем,
как мы осуществляем обучение младших школьников приемам умственной деятельности
на примере решения задач-головоломок с палочками.
В
ходе обучения мы выделили пять последовательных этапов в развитии поисковых
действий.
На
первом этапе у детей формировалось умение воспринимать задачу
(что надо сделать) и в результате практических поисков приходить к решению
(составить, видоизменить фигуру), видеть и называть получившиеся геометрические
фигуры (квадрат, треугольник, четырехугольник, многоугольник и т.д.), понимать
значение слова «общая» по отношению к стороне, «смежная» — для двух фигур, а
также значение слова «присоединил», говоря о способе составления.
Для
этого можно использовать задачи на составление фигур из палочек. Составить:
1)
флажок,
лопатку из 5 палочек;
2)
домик
из 6 палочек;
3)
2
равных треугольника из 5 палочек;
4)
2
равных квадрата из 7 палочек;
5)
3
равных треугольника из 7 палочек;
6)
3
равных квадрата из 10 палочек;
7)
4
равных треугольника из 9 палочек;
8)
из
5 палочек квадрат и 2 равных треугольника.
Решение
состоит в пристраивании к одной фигуре другой (из меньшего количества палочек)
или в делении одной фигуры для получении новой.
Педагог
предварительно предлагает детям наметить возможные построения, обучая детей
частичному планированию поиска в уме. У ребенка должна возникнуть идея и способ
решения (какие палочки и куда положить). На этом этапе обучения можно научить
детей осуществлять осознанные практические действия, отбрасывать способы, не
приводящие к правильному решению, не бояться необычных подходов. В результате у
детей воспитывается гибкость, подвижность мышления.
На
втором этапе обучения ставятся новые цели: учить детей рациональному способу
решения задач (преобразованию). Постепенно способ решения задач путем проб и
ошибок должен быть заменен более эффективным, основанным на предварительным
обдумывании, выдвижении предположений. На этом этапе педагог иначе руководит
процессом решения задачи. Если на первом этапе обучения он поощрял пробные
ориентировочные действия ребенка, то теперь он предлагает проанализировать
задачу, высказать предположения, прежде чем действовать практически. Анализ
состоит в пересчитывании фигур, из которых составлена задача, самостоятельном
выделении необходимых преобразований. Затем педагог предлагает подумать, как
нужно решать задачу, высказать свое предположение, а затем проверить его
практически. Необходимо так организовать руководство процессом поиска решения,
чтобы при анализе практических проб ребенок пришел к идее решения и высказал
ее. Если решение ошибочно, он должен убедиться в этом и искать новый путь.
На
этом этапе содержание задач усложняется. Используются такие задания, для
которых надо убрать заданное количество палочек.
Задача
1.
В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4
квадрата. (Слева изображена начальная конфигурация, справа — ответ.)
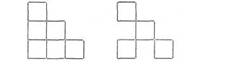
Задача
2. В
фигуре из 5 квадратов убрать 3 палочки, чтобы осталось 3 квадрата. (Слева
изображена начальная конфигурация, справа — ответ.)
![]()
Третий
этап обучения
направлен на то, чтобы постепенно подводить детей к решению задач в уме. Детям
предлагают: «Рассмотрите составленную фигуру. Подумайте, что надо сделать и
как. Сначала скажите, как вы собираетесь решать задачу. Проверьте правильность
этого способа решения и только потом перекладывайте палочки». Для развития
творческой мыслительной деятельности надо учить детей догадываться о решении.
Это возможно при глубоком понимании постановки задачи. Педагог предлагает:
«Подумай и догадайся, как решить эту задачу».
На
третьем этапе даются задачи на более сложные преобразования.
Задача
3. Из
9 спичек сложите весы (как на рисунке слева). Переложив 5 спичек, сделайте так,
чтобы весы оказались в состоянии равновесия. (Ответ дан на рисунке справа.)
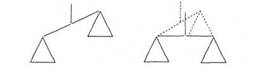
На
четвертом этапе даются задания на добавление
необходимого числа палочек к исходной фигуре для получения нужного результата.
Подобные задачи часто имеют несколько решений.
Задача
4. Изгородь
квадратного сада составлена из 16 спичек. В саду расположен дом, представленный
квадратом из 4 палочек, как на рисунке слева. Взяв еще 10 спичек, попробуйте
разделить сад (без дома) на 5 равных одинаковых участков. (Ответ
дан
на рисунке справа.)
![]()
На
пятом этапе детям предлагается самостоятельно сконструировать
подобные задачи, представить свой проект и организовать решение составленной
задачи.
Проведенная
работа и ее результаты позволяют сделать вывод о том, что систематическое
решение эвристических задач на внеклассных занятиях является эффективным
средством повышения интереса детей к обучению математике, развития их
умственной инициативы и творческой активности.
Заключение
Таким
образом, трудно переоценить роль математики в обучении и развитии мышления и
познавательной активности школьников. Благодаря прикладной особенности
математический аппарат используется при изучении различных предметов, что
способствует их более глубокому усвоению. При этом активизируется учебная
деятельность школьников, в процессе которой они овладевают методами познания,
расширяется их кругозор и формируется научное мировоззрение. Работа выполнена с
целью изучить, какие актуальные методы и приемы решения задач, используемые в
современных начальных школах, позволяющие детям осознанно решать задачи. Возможности
формирования общеучебных умений при решении текстовых задач рассматривается
процесс решения задач как переход от словесной модели к математической.
В
основе этого перехода лежит семантический (смысловой) анализ текста и выделение
в нем математических понятий и отношений (математический анализ текста).
Учащиеся должны быть подготовлены к этой деятельности. Выделяются основные
свойства осознанности: осмысление связей и отношений между знаниями; осознание
одних знаний как базовых для других знаний. Это позволило в ходе исследования
конструировать эти связи и отношения между текстовыми задачами, а также
выделять или составлять базовую (основную) задачу по теме. В результате было
сформулировано определение метода варьирования текстовых задач и определение
базовой задачи.
Метод
варьирования текстовых задач — это способ конструирования из
одной задачи (назовем ее базовой) цепочки взаимосвязанных задач.
Наиболее
успешно дети справлялись с решением задач логического типа, в которых им был хорошо
знаком или материал , или операции. Задачи, требующие исключительно внутреннего
плана действий, установления сложных отношений, перестановки и комбинирования
простых элементов, перебора вариантов, решались на первых порах с большим
трудом. Однако следует отметить, что именно эти действия особенно заметно
прогрессировали в процессе работы.
Литература
1. Давыдов.
В.В. Содержание
и структура учебной деятельности школьника / В.В. Давыдов // Формирование
учебной деятельности школьника ; под. ред. В.В. Давыдова и др. — М. :
Педагогика, 1982.
2. Еленьска
Л. Методика
изучения арифметики и геометрии. М., 1960.
3. Зайцева.
СЛ. Методика
обучения математике в начальной школе : учебно-метод. пос. / С.А. Зайцева, И.И.
Целищева, И.И. Румянцева. — М. : Владос, 2008. — 192 с.
4. Иванова
Т.С. Экологическое
образование и воспитание в начальной школе. М., 2003.
5. Истомина
Н.Б. Методические возможности калькулятора при обучении младших школьников
математике. – М.: Просвещение, 2000 г. — 110 с.
6. Крутецкий
В.А. Психология
математических способностей школьников. М.; Воронеж, 1998.
7. Моро
М.И. и др. Математика: Учеб. для IV
кл. Ч. 2. М., 2002.
8. Моро
М.И. Пышкало А.М. Методика обучении математике в 1-4 классах. – М.:
Просвещение,1995 г.
9. Смирнова
А.А. Метод
варьирования текстовых задач по математике как средство повышения качества
знаний учащихся: Дис. канд. пед. наук. СПб., 2007.
10. Тарасов
JI.B.
Модель
школы «Экология и диалектика» // Школьные технологии. 1997. №1.
11. Фоминых
Ю.Ф., Худякова МЛ. Перспективы преподавания математики по
обогащающей модели // Проблемы и перспективы развития методики обучения
математике. СПб., 1999. Фоминых Ю.Ф., Худякова МЛ. Роль обучающих заданий в
повышении математической компетентности учащихся // Содержание и методы
обучения математике в школе и вузе на рубеже столетий: исторический и методологический
аспекты. Брянск, 2000 г.
12. Фридман.,
JI.M.
Наглядность
и моделирование в обучении / Л.М. Фридман. — М. : Знание, 1984. Целищева, И.И. Использование
моделирования в процессе работы с текстовой задачей в 1 классе / И.И. Целищева,
С.А. Зайцева // Начальная школа. — 2008. — № 1. — С. 55-63. Целищева., И.И.
Моделирование простых текстовых задач: уч. Пос. /И.И. Целищева, С.А. Зайцева.
М.: Чистые пруды, 2006. – 32 с. (Библиотечка «Первое сентября», серия
«Начальная школа»). Целищева. И.И. Организация работы над текстовой задачей на
основе модели / И.И. Целищева, С.А. Зайцева. // Начальная школа. — 2007. — № 4
— 6. Фридман Л.М. Логико- психологический анализ школьных учебных задач. –М.:
Просвещение, 1991 Эрдниев П.М. взаимообразные действия в математике. – М.:
Просвещение,1991 г. — 254 с.
13. Эрдниев
П.М. Фактор
времени в процессе обучения и проблема «укрупнения единицы усвоения знания» //
Вопросы философии. 1974. №4.
14. Лесная
газета. 2005. № 61 (9607). Июль.- с. 15
