Задание 1. По исходным данным построить дискретный ряд распределения по группировочному
признаку. Для целей анализа и сравнения применить характеристики центра группирования,
к которым относятся средняя арифметическая, мода и медиана. Для характеристики степени
отклонения распределения частот от симметричной формы рассчитать показатели эксцесса
и ассиметрии. Проанализировать полученные значения показателей центра распределения
и формы распределения. Сформулировать вывод.

Таблица 1 —
Основные показатели деятельности предприятия за период «N»

№ п/п	Выручка от продажи товаров, т.р.	Прибыль от продаж, т.р.	Чистая прибыль отчетного периода,т.р.	Основные средства,т.р.	Запасы, т.р.	Денежные средства, т.р.
4	344280	24774	22364	106447	28423	6329
5	107843	9210	7850	92805	26458	1341
6	105600	4678	5076	52187	9844	3107
7	198771	13115	11429	46234	82938	2011
8	85000	4809	5862	56932	27850	1329
9	62000	2381	1523	47067	26781	1378
10	171647	65920	24971	54356	21342	1901
11	45499	7659	8124	29351	84013	6082
12	110690	4817	1478	62651	10328	1638
13	32106	1089	941	40633	23805	4999
14	71587	20995	18180	64567	11774	1576
15	21980	5515	3030	58711	11559	2387
16	24690	10786	13123	87210	32952	6031
17	56341	3412	2271	57195	20645	1299
18	56000	2014	2017	33465	54864	3757
19	45700	7469	6154	32176	23256	6222
20	183600	38983	1170	11553	76561	8854
21	21197	2586	2189	40150	13942	1537
22	24446	6310	1776	13488	74681	3136
23	29520	8336	1621	39282	33516	1006
24	48370	8657	9882	19107	15197	2232
25	75650	17815	1235	18184	28310	2810
26	31430	1526	8882	62741	40355	1277
27	256050	9250	4813	20705	39373	1085
28	86830	6545	1653	72342	15002	6701
29	50002	4908	4589	14546	47844	1202
30	38654	3016	1579	22661	27833	7555
31	83761	20950	1570	23480	17210	4393
32	61235	27133	1321	25590	19700	4400
33	55320	11500	1754	18650	20600	3650

Распределение
варианта заданий 1и 2.

Номер варианта	Номер предприятий	Результативный признак	Группировочный признак
4	4-33	Прибыль от продаж	Основные средства

Построим дискретный
ряд по группировочному признаку, в нашем случае группировочный признак основные
средства:

Таблица 2.
— Дискретный ряд

№ п/п	Прибыль от продаж, т.р.	Основные средства, т.р.
4	24774	106447
5	9210	92805
6	4678	52187
7	13115	46234
8	4809	56932
9	2381	47067
10	65920	54356
11	7659	29351
12	4817	62651
13	1089	40633
14	20995	64567
15	5515	58711
16	10786	87210
17	3412	57195
18	2014	33465
19	7469	32176
20	38983	11553
21	2586	40150
22	6310	13488
23	8336	39282
24	8657	19107
25	17815	18184
26	1526	62741
27	9250	20705
28	6545	72342
29	4908	14546
30	3016	22661
31	20950	23480
32	27133	25590
33	11500	18650

Величина интервала
группировки определяется по формуле:

,

где d – величина
интервала, k – число групп, R – размах вариации, x_max— максимальное значение группировочного
признака в совокупности, x_min— минимальное значение группировочного признака.

x_max=106447; x_min=11553

=23723,5

В результате
подсчета предприятий в каждой группе получим ряд распределения предприятий по размеру
основных средств. Минимальное значение признака совпадает с верхней границей первой
группы, а максимальное значение признака совпадает с нижней границей четвертой группы.
Рассчитаем показатели центра распределения: x, Мо, Ме. Среднюю величину в интервальном
ряду распределения определим по формуле средней арифметической взвешенной:

,

Х – Средняя
величина; x’_i – среднее значение признака в интервале (центр интервала),
f_i – число единиц совокупности в интервале (частота).

X= =44762,9

Результаты группировки
предприятий по размеру основных средств:

Группа п/п по размеру основных средств, xi	Число предприятий ,fi	Середина интервала, x’i	x’i×fi	Накопленная частота, Si
11553 — 35276,5	13	23414,75	304391,75	13
35276,5 – 59000	10	47138,25	471382,5	23
59000 – 82723,5	4	70861,75	283447	27
82723,5 – 106447	3	94585,25	283755,75	30
30	1342977

Мода – наиболее
часто встречающееся значение признака в совокупности. Для определения величины
моды используют следующую формулу:

Мо= x_Мо+d ,

где x_Мо – начало модального
интервала; f_Мо – частота, соответствующая модальному интервалу; f_{Мо — 1}
– предмодальная; f_Мо+1 – послемодальная.

Мо=11553+23723,5 =11553+23723,5 =30828,34

Для определения
величины медианы используем следующую формулу:

Ме=x_Ме+d( -S_{Ме — 1})/f_Ме,

где x_Ме
– нижняя граница медианного интервала; S_{Ме — 1} – накопленная частота интервала,
предшествующая медианному; f_Ме— частота медианного интервала.

Ме=11553+23723,5 =38926,27

Выяснение общего
характера распределения включает также оценку степени однородности, а также вычисление
показателей ассиметрии (А_s) и эксцесса (Е_s). Простейший показатель
ассиметрии основан на соотношении показателей центра распределения: чем больше разница
между средними (x-Мо), тем больше ассиметрия ряда. В нашем случае 44762,9 – 30828,34
=13937,56.

Величина показателя
ассиметрии в нашем примере положительная , что указывает на наличие правосторонней
ассиметриии (Мо<Ме<x): 30828,34<38926,27<44762,9.

Задание 2. Для выявления зависимости между экономическими показателями деятельности
предприятий провести аналитическую группировку показателей 30 предприятий. Группировку
провести с равными интервалами, выделив четыре группы. Рассчитать коэффициенты вариации
по группировочному признаку на основании исходных данных и по аналитической группировке
согласно своего варианта. Объяснить расхождения в значениях полученных коэффициентов.

Таблица 3.
— Распределим предприятия по величине основных средств.

№ п/п	Основные средства, т.р.	№ п/п	Основные средства, т.р.
4	106447	19	32176
5	92805	20	11553
6	52187	21	40150
7	46234	22	13488
8	56932	23	39282
9	47067	24	19107
10	54356	25	18184
11	29351	26	62741
12	62651	27	20705
13	40633	28	72342
14	64567	29	14546
15	58711	30	22661
16	87210	31	23480
17	57195	32	25590
18	33465	33	18650

Величина интервала
группировки определяется по формуле:

,

где d – величина
интервала, k – число групп, R – размах вариации, x_max— максимальное значение группировочного
признака в совокупности, x_min— минимальное значение группировочного признака.

x_max=106447; x_min=11553

=23723,5

В результате
подсчета предприятий в каждой группе получим ряд распределения предприятий по размеру
основных средств. Минимальное значение признака совпадает с верхней границей первой
группы, а максимальное значение признака совпадает с нижней границей четвертой группы.

Таблица 1-
Распределение предприятий по размеру основных средств

Номер группы	Граница
	нижняя	верхняя
1	11553	35276,5
2	35276,5	59000
3	59000	82723,5
4	82723,5	106447

Таблица 2Группировка
предприятий по величине основных средств.

Группы предприятий по величине основных средств, тыс.руб	Число предприятий в группе	Предприятие	Всего по группе, тыс.руб	Средний размер основных средств по группе, тыс.руб.
11553 — 35276,5	13	11,18,19,20,22,24,25,27,29,30,31,32,33	282956	21765,85
35276,5 – 59000	10	6,7,8,9,10,13,15,17,21,23	492747	49274,7
59000 – 82723,5	4	12,14,26,28	262301	65575,25
82723,5 – 106447	3	4,5,16	286462	95487,33
Итого	30	1324466	44148,87

Таблица 3.
— Расчет показателей вариации для предприятий, сгруппированных по величине основных
средств.

Группы предприятий по величине основных средств, млн.руб	Число п/п fi	Расчетные показатели
		xi‘	xi‘ fi	xi‘-x	(xi‘-x)2 fi
11,5 – 35,3	13	23,4	304,2	— 21,34	5920,14
35,2 – 59,0	10	47,1	471,0	2,36	55,69
59,0 – 82,7	4	70,8	283,4	26,06	2716,5
82,7 – 106,4	3	94,6	283,7	49,86	7458,05
Итого	30	1342,3	16150,38

Рассчитаем коэффициенты
вариации для исходным данным и по аналитической таблице. Среднее по исходным данным:

X= = =44,15 млн. руб.

По сгруппированным
данным:

X= 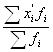= =44,74 млн. руб.

Среднее квадратичное
по исходным данным:

σ= =37,53 млн. руб.

Среднее квадратичное
отклонение по сгруппированным данным:

σ= =23,20 млн. руб.

Находим коэффициент
вариации по формуле:

ν=

Коэффициент
вариации по исходным данным:

ν= *100%=85%

Коэффициент
вариации по сгруппированным данным:

ν= =51,86%

В обоих расчетах
коэффициент вариации значительно больше 33%. Следовательно, рассмотренная совокупность
неоднородна и средняя для нее недостаточна типична.

Задание 3. Выполнить анализ показателей бухгалтерского баланса (Форма 1) путем
расчета показателей структуры и динамики. Данные для выполнения задания взяты по
ООО торговый дом «Светлый» на 30.07.2008г. По результатам расчетов охарактеризовать
основные тенденции изменения структуры в динамике. Для выполнения аналитических
исследований и оценок структуры актива и пассива баланса произвести группировку
его статей.

Таблица 4 –
Статьи баланса

Статьи баланса	Базисный период		Отчетный период		Отклонения		Динамика отчетного периода в % к базисному
	Сумма, тыс.руб.	Удельный вес, %	Сумма, тыс.руб.	Удельный вес, %	В сумме, тыс.руб.	В процентах, %
А	1	2	3	4	5=3-1	6=4-2	7=3/1*100%
Внеоборотные активы	554	8,8	496	8,5	— 58	— 0,3	89,5
Оборотные активы	5732	91,2	5346	91,5	— 386	— 0,3	93,3
Баланс	6286	100,0	5842	100,0
Капитал и резервы	2969	47,2	3444	59,0	475	11,8	116,0
Долгосрочные обязательства	0	0	0	0	0	0	0
Краткосрочные обязательства	3317	52,8	2398	41,0	— 919	— 11,8	72,3
Баланс	6286	100,0	5842	100,0

Для характеристики
интенсивности изменения во времени к таким показателям относят:

Абсолютный прирост;

Темп прироста;

Темп роста;

Коэффициент роста.

Когда сравнение
проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные
показатели; при сравнении же с предыдущим периодом или моментом времени речь идет
о цепных показателях.

Задание 4.Провести 25% механическую выборку из генеральной совокупности по показателю,
который является для нас результативным. С вероятностью 0,954 рассчитать границы
изменения средней величины в генеральной совокупности и сравнить с результатом,
полученным на основании расчета по выборочной совокупности. Начало отбора начинать
с номера предприятия совпадающего с номером варианта. Сформулировать вывод.

Выборочный метод
применяется в тех случаях, когда проведение наблюдения невозможно или экономически
нецелесообразно.

Часть единиц,
отобранных для наблюдения, принято называть выборочной совокупностью, а всю совокупность
единиц, из которых производится отбор, — генеральной. Качество результатов выборочного
наблюдения зависит от того, насколько состав выборки представляет совокупность.

По заданию следует
начать с номера предприятия, совпадающего с номером варианта. При 33% выборке шаг
отсчета (1/0,33) равен 3.

Номер предприятия	Основные средства, млн. руб.	Расчетные показатели
		x-x	(x-x)2
4	106,45	57,0	3249
7	46,23	— 3,22	10,36
10	54,36	4,91	24,11
13	40,63	— 8,82	77,79
16	87,21	37,76	1425,82
19	32,18	— 17,27	298,25
22	13,49	— 35,96	1293,12
25	18,18	— 31,27	977,81
28	72,34	22,89	523,95
31	23,48	— 25,97	674,44
Итого	494,55	8554,65

Величина средней
ошибки механического бесповторного отбора для малых выборок определяется по упрощенной
формуле:

µ_x
= ,

где N – объем
генеральной совокупности (число входящих в нее единиц), n=10 – объем выборки (число
обследованных единиц), S² – выборочная дисперсия (дисперсия признака
в выборочной совокупности).

Наиболее часто
употребляемые уровни доверительной вероятности и соответствующие значения отношения
Стьюдента (коэффициента доверия) t при числе степеней свободы k=n – 1 = 9:

P	0,9	0,95	0,98	0,99	0,999
t	1,740	2,110	2,567	2,898	3,965

Для расчета
границ изменения средней характеристики генеральной совокупности по материалам выборки
воспользуемся следующими формулами:

x= x±∆

∆ = t µ_x

(x – средняя
выборочной совокупности;

x – средняя
генеральной совокупности;

∆ — предельная
ошибка выборки;

µ_x
– средняя ошибка выборки).

Средняя стоимость
основных средств на одном предприятии по выборочной совокупности равна:

x =  млн. руб.

дисперсия S²
=855,47; t = 3,965; n/N = 0,33, т.к. процент отбора составляет 33%.

µ_{x =}

Рассчитаем предельную
ошибку и определим границы изменения средней:

∆= 3,965
*7,98=31,64

49,45 — 31,64
<x<49,45+31,64

17,81<x<81,09

Таким образом,
с вероятностью 0,999 можно утверждать, что стоимость основных средств на одном предприятии
в генеральной совокупности будет находиться в пределах от 17,81 млн. руб. до 81,09
млн. руб.

Задание 5. По данным своего варианта исчислить: Базисные, цепные и среднегодовые
показатели абсолютного прироста, темпов роста и темпов прироста объемов индивидуального
жилищного строительства.

Среднегодовой объем индивидуального жилищного
строительства.

Изобразить динамику индивидуального жилищного
строительства на графике.

Таблица 5 —
Данные об объеме индивидуального жилищного строительства по району

Период в годах, год	Объем индивидуального жилищного строительства, м2 общей площади
1989	234
1990	240
1991	242
1992	258
1993	267
1994	457
1995	480
1996	632
1997	718
1998	1319

Динамический ряд представляет собой ряд последовательных уровней, сопоставляя
которые между собой можно получить характеристику скорости и интенсивности развития
явления. В результате сравнения уровней получается система абсолютных и относительных
показателей динамики, к числу которых относятся абсолютный прирост, темп роста,
темп прирос та, абсолютное значение одного процента прироста и пункты роста.

Абсолютный прирост (∆_i ) определяется как разность
между двумя уровнями динамического ряда. При сравнении с постоянной базой он равен:

∆_i
баз= Y_i – Y₀

где∆_{i баз} — абсолютный прирост базисный; У₁
— уровень сравниваемого периода; У₀ — уровень базисного периода.

При сравнении с переменной базой

∆_i
= Y_i – Y_{i — 1}

Где ∆_i — абсолютный прирост цепной; Y_{i — 1}
— уровень непосредственно предшествующего периода. Темп роста определяется
как отношение двух сравниваемых уровней. Пои сравнения с постоянной базой

Тр= (Y_i
: Y₀) * 100

При сравнении
с переменной базой

Тр= (Y_i
: Y_{i — 1}) * 100

Темп прироста показывает на сколько процентов уровень данного пе риода
больше (или меньше) базисного уровня.

Тпр=  или Тпр =

а также как разность между темпом роста (в процентах) и 100%

Тпр = Тр – 100%

Рассчитаем все показатели по
ряду динамики, характеризующему объем индивидуального жилищного строительства. Данные
расчета представить в таблице:

Таблица 6 —
Показатели по ряду динамики

Год	Общая площадь, м2	Абсолютный прирост (∆)		Темп роста, % (Тр)		Темп прироста, % (Тпр)
		цепной	базисный	цепной	базисный	цепной	базисный
1989	234	—	0,0	—	100	0,0	0,0
1990	240	6	6	102	102	2	2
1991	242	2	8	101	103	1	3
1992	258	16	24	106	110	6	10
1993	267	9	33	103	114	3	14
1994	457	190	223	171	195	71	95
1995	480	23	246	105	205	5	105
1996	632	152	398	132	270	32	170
1997	718	86	484	114	307	14	207
1998	1319	601	1085	184	564	84	464

Рассчитаем средние
показатели:

а) средний уровень:
Y= м²

б) средний абсолютный
прирост:

∆= м²

в) среднегодовой
темп роста по формуле среднегеометрической:

Тр=

Рассчитанные
аналитические показатели характеризуют состояние объема индивидуального жилищного
строительства за 1989 – 1998 годы. Абсолютный прирост показывает скорость увеличения
объемов строительства по сравнению с 1989 годом он составил 1085 м².
Темп роста показывает, что объем строительства 1998 года составил 564% от уровня
базисного года (1989). Темп прироста дает возможность оценить на сколько процентов
объем строительства в 1998 увеличился по сравнению с 1989 – 464%.

Задание 6. По данным своего варианта определить:

Общие индексы:

а) цен;

б) физические
объемы проданных товаров,

в) товарооборота.

Какую роль в
изменении товарооборота сыграли изменения цен и количества проданных товаров?

Абсолютную величину изменения расходов населения
в связи с изменением цен.

Таблица 7 —
Реализация товаров в магазине

Вид товара	Предыдущий период		Отчетный период
	Кол-во, шт.	Цена за единицу, руб.	Кол-во, шт.	Цена за единицу, руб.
Ноутбук Монитор	10 8	6500 3200	14 12	5500 3400

Общий индекс
цен рассчитываем по формуле:

J_p
=

Цены на оба
товара снизились в среднем на 9%

Общий индекс
физического объема товарооборота (количество проданного товара) находим по формуле:

J_q
=

Количество проданного
товара отчетном периоде было продано больше на 42,8%, чем в предыдущем.

Теперь рассчитаем
общий индекс товарооборота:

J_pq
=

Товарооборот
увеличился в отчетном периоде на 30% по сравнению с предыдущим периодом.

Увеличение товарооборота
произошло за счет уменьшения цены:

∑p₁q₁
— ∑p₀q₁=117800 – 129400 = — 11600 руб.

В тоже время
увеличение товарооборота произошло за счет изменения количества проданного товара:

∑p₀q₁
— ∑p₀q₀ = 129400 – 90600 = 38800руб.

Следовательно,
увеличение товарооборота на 11600 руб. произошло за счет увеличения проданных товаров
на 38800 руб. и за счет уменьшения роста цен на 27200 (38800 + ( — 11600) = 27200
руб.).

Задание 7. Для выявления зависимости между группировочным и результативным показателями
рассчитать линейный коэффициент корреляции по исходным данным.

№ п/п	Основные средства, млн.руб. (группировочный признак) (x)	Выручка от продажи товаров, млн.руб. (результативный признак) (y)	xy	x2	y2
4	106	344	36464	11236	118336
5	93	107	9951	8649	11449
6	52	105	5460	2704	11025
7	46	198	9108	2116	39204
8	57	85	4845	3249	7225
9	47	62	2914	2209	3844
10	54	171	9234	2916	29241
11	29	45	1305	841	2025
12	63	110	6930	3969	12100
13	41	32	1312	1681	1024
14	64	71	4544	4096	5041
15	59	21	1239	3481	441
16	87	24	2088	7569	576
17	57	56	3192	3249	3136
18	33	56	1848	1089	3136
19	32	45	1440	1024	2025
20	11	183	2013	121	33489
21	40	21	840	1600	441
22	13	24	312	169	576
23	39	29	1131	1521	841
24	19	48	912	361	2304
25	18	75	1350	324	5625
26	63	31	1953	3969	961
27	20	256	5120	400	65536
28	72	86	6192	5184	7396
29	14	50	700	196	2500
30	22	38	836	484	1444
31	23	83	1909	529	6889
32	25	61	1525	625	3721
33	18	55	990	324	3025
Итого	1317	2572	127657	75885	384576

По данным о
стоимости основных фондов и выручке от продаж товара необходимо оценить тесноту
связи.

Расчеты парного
коэффициента корреляции следует произвести по следующей формуле:

r =

или

r =

где x, y – индивидуальные
значения факторного и результативного признаков; x, y – средние значения признаков;
xy – средняя из произведений индивидуальных значений признаков; σ_x,
σ_y – средние квадратические отклонения признаков.

Рассчитаем величину
линейного коэффициента корреляции:

r =

Коэффициент
парной корреляции близок к единице, можно говорить о тесной связи изучаемых признаков.

Список используемой
литературы

1. Елисеева,
И.И. Общая теория статистики: Учебник для вузов / И.И. Елисеева, М.М. Юзбашев. —
5-е изд. Пер. и доп. — М.: Финансы и статистика, 2004. — 656 с.

2. Ефимова,
М.Р. Общая теория статистики / М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцев. — М.:
ИНФРА-М, 1997. — 416 с.

3. Ефимова,
М.Р. Практикум по общей теории статистики : Учеб. пособие / М.Р. Ефимова, О.И. Ганченко,
Е.В. Петрова. — М.: Финансы и статистика, 1999. — 280 с.

4. Общая теория
статистики. Статистическая методология в изучении коммерческой деятельности / Под
ред. О.Э. Башиной и А.А. Спирина. — М.: Финансы и статистика, 2001. — 440 с.

5. Сборник задач
по общей теории статистики. Учеб. пособие / Под ред. к.э.н. Л.К. Серпа.- — М.: Инф.-
изд. дом Филинъ, 1999. — 360 с.

6. Статистика:
Учебное пособие / Под ред. В.Г. Ионина. — 2-е изд. пер и доп. — М.: ИНФРА-М,
2002. — 384 с.

7. Статистика:
Учеб. пособие / Под ред. М.Р. Ефимовой. -М.: ИНФРА-М, 2002. — 336 с.

8. Сборник задач
по теории статистики / Под ред. В.В. Глинского — М ‘ ИНФРА-М, 2002. — 257 с.

9. Теория статистики:
Учеб для вузов / Под ред. Р.А. Шмойловой. — 3-е изд. перер. — М.: Финансы и статистика,
2002. — 560 с.